We invented math to describe natural phenomena around us. If Grogg has 4 stones, and you gave him 12 more, he would have 16 stones. This is fundamental and logical.
What is almost magical and impossible, though, are the ways in which math shows up in nature. For example, the spirals on a pinecone follow the Fibonacci sequence.

Photo by Jennifer Burk on Unsplash
It seems the Fibonacci and fractals cannot disconnect themselves from nature and art. There is something aesthetically pleasing, and perhaps even life-sustaining about these patterns.
First of all, what are fractals, and what is the Fibonacci sequence anyway?
Both of them rely on the concept of recursion. Have ever seen or heard of a Russian nesting doll? The way they work is there are multiple dolls inside of one another. When you open the first, there is another doll inside, and so on and so on, getting smaller and smaller. It almost seems like there are infinitely many and it will never end.
If that makes any sense to you, then you understand recursion!

Fractals:
They are objects which contain themselves.
Period.
Okay, that’s not a very helpful explanation.
Here is a picture.

It has a special name: Serpinski’s Triangle!
If you zoom into the image, you will actually see a smaller version of the image itself. It has this "infinite-property." You can keep zooming in, but you will still see the same image.
Here is another example:

Source: Pinterest
Believe it or not: this snowflake has a finite area, but infinite perimeter. The absurdity of fractals lies in the palm of our hands!
Why?
Imagine you were an ant walking along the edge of this snowflake. You would up a tiny bit, then down, then forward, then backwards. When your account for the infinite granularity of a fractal, the path has infinitely more twists and turns. That is why the perimeter is so large (and actually infinite!).
If you were the same ant, however, and wanted to walk from one side of the snowflake to the other, you could do so easily. Hence, a snowflake has infinite perimeter and a finite area.
This is our first illustration of fractals in nature. Although this is not a real snowflake, snowflakes do naturally form as fractals (or at least very close to being fractals).
Okay, so now I know what fractals are, but what is the Fibonacci sequence?
The Fibonacci sequence is an infinite sequence of integers. The first two numbers are 1 and 1. Each next term is the sum of the two before. For example, the third term is 2, the fourth is 1+2=3, the fifth is 2+3=5, the sixth is 3+5=8 and so on.
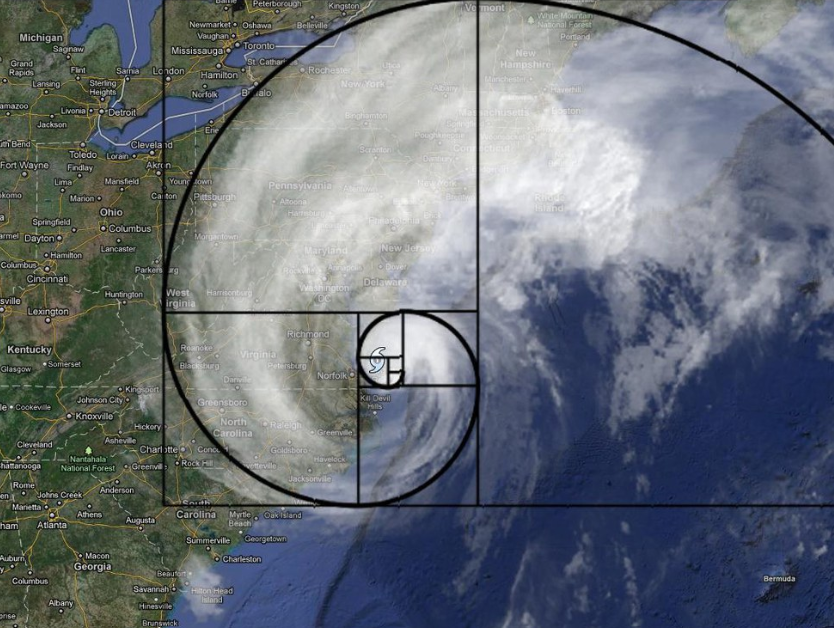
Another feature of the Fibonacci sequence is the golden ratio. It is found by dividing a term in the sequence by the previous term. For example, with the first two it is 1/1=1, next is 2/1 =2, then 3/2, then 5/3, 8/5. Interestingly enough, this quotient gets closer and closer to a specific value known as phi or the golden ratio. This ratio has been used in famous art and can also be found in nature as well.
Whenever you take a walk in the park, or go to your local art museum, get an eye out for fractals, the Fibonacci sequence, and the golden ratio. You will not be disappointed.
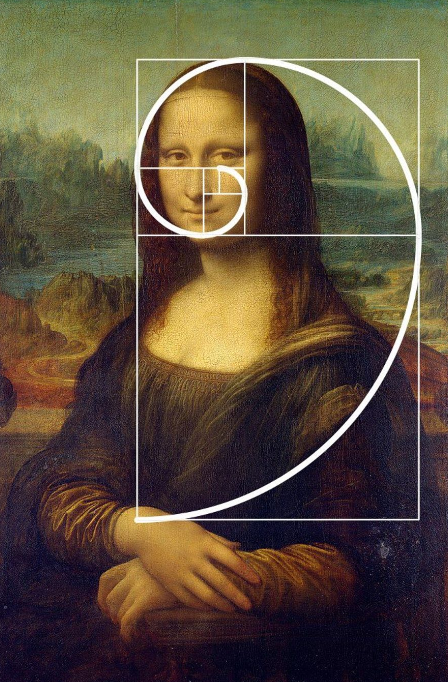

Ferns are great examples of fractals in nature
Photo by CHUTTERSNAP on Unsplash

Many succulents are also natural fractals

This sea shell demonstrates the curve of the golden ratio

And it naturally appeals to our eye in art:
(Hokusai, The Great Wave off Kanagawa, 1831)

Comments